
Any finite set of equations (E) can be called a system. These systems (SE) arise when solving problems in mathematics, physics and other sciences, where not one value is unknown, but several. These quantities are related by certain dependencies, which are written as equations.
Next, you will learn how to find solutions in such SE.
How to Solve Systems of Equations by Elimination?
If a system has at least one solution, it is called compatible. If a system has no solutions, it is called incompatible. The word “incompatibility” clearly shows that different E of a system impose incompatible conditions with each other, which should satisfy the unknown. In general, we can consider systems of m E with n unknowns, in which all three cases are possible: m=n , m
The elimination math method is based on the principle of equality of both parts of E, provided that the same numerical values are added to them. So if a=b and c=d, then a+c=b+d. Everything is simple.

However, there are systems that are not so easy. You must first select a variable that you will need to exclude. And then you must choose such a factor (for one or two E at once), so that the coefficients of the chosen variable become opposite.
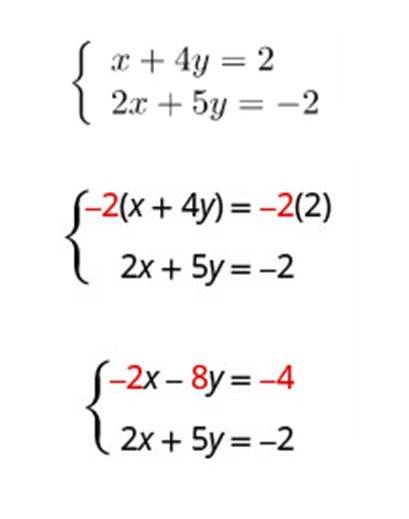
We took the variable x and multiplied the first E of our system by –2. Then we perform the addition. And we receive у=2.
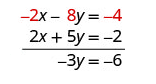
By the way, you will not be able to master this method without solving dozens of significantly more complex systems than shown in the example above. Therefore, if you have any questions, we recommend you use the help of a teacher. This may be courses or a private tutor – of your choice. Americans quite often prefer the UpskillsTutor site, where you can select a tutor with decent professional characteristics exclusively for your educational needs.
Read more: 8 Tips for Using the TI-84 Graphing Calculator on the SAT
Substitution Method: Examples with Answers
This is a method of solving SE by deleting all but one of the variables in one of the E, and then solving that E. Some systems of cubic E (as well as systems that include Е of degrees higher than cubic) are convenient to solve using the replacement of variables. This method can be applied in two ways:
- one new variable is introduced and used only in one E of a system;
- two new variables are introduced and used simultaneously in both E of a system.
Turn to the substitution method example.
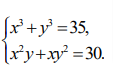
Notice that the left-hand sides of E of a system are symmetrical polynomials. Let us introduce a replacement х+y=u; ху=у. Due to the replacement, the system will look like:
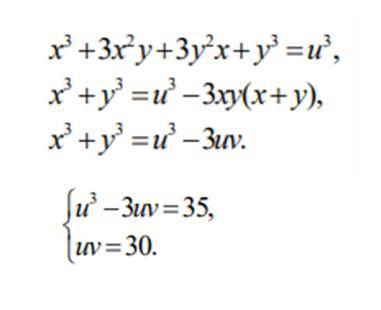
Then we solve the last system using substitution. After that, we return to our change. To obtain the final results, we should apply the theorem inverted to the Viet theorem:
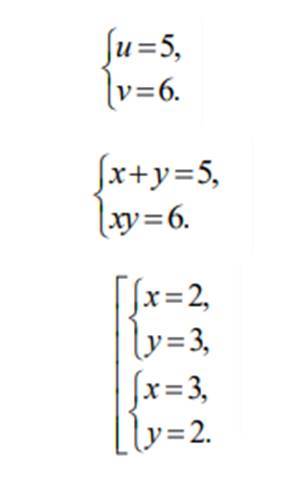
In summary, we have the answer: (2; 3), (3; 2).
Graphical Method of Solving: How Effective It Is
The graph of each E of a system of linear E with two variables is a straight line.
- If lines intersect, a system has a single solution.
- If lines do not intersect, then a system has no solutions.
- If lines match, a system has many solutions.

Construct graphs of E of a system in one coordinate plane. Find the coordinates of the intersection point of the graphs of E. In the picture below, this is the M (1;2) point.

The graphical way of solving SE is not universal, since not always the solution of a system is a pair of integers. Sometimes it is difficult to accurately set the coordinates of the intersection point of the plotted graphs of functions, it is possible only to specify the approximation value. How to find a solution to the system of equations in this case?
The most efficient way is to clarify all the unclear moments during individual classes with a tutor. This topic is not very suitable for self-study, at least for in-depth study. As a rule, algebraic methods are applied, such as substitution or addition already mentioned.




